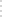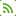По-моему Кубиком Рубика (Rubik's Box) уже никого не удивишь. Это, наверное, одна из самых известных и узнаваемых логических игрушек. Изобретенный в 1974 году Венгерцем Эрнё Рубиком. Это был пластмассовый кубик 3 × 3 × 3. И изначально он назывался как “Магический кубик”. С тех пор прошло уже много времени, была сделана куча попыток усовершенствовать кубик Рубика, его даже делали 5 × 5 × 5, Круглым, Пирамидальным и даже змейкой. Но, не смотря на то, что прошло уже столько лет, и появилось большое количество не менее интересных игрушек, множество поколений бьется над тем как же всё же собрать Кубик Рубика. Самые “сообразительные” переклеивали цветные квадратики. Или же разбирали его и составляли, так как нужно. Но всё гораздо проще, сегодня я представлю вам несложную формулу в картинках, используя которую собрать Кубик Рубика сможет каждый желающий.


Всё просто, главное понять то, что на схеме 3x3 всегда изображена передняя часть Кубика Рубика. А стрелками обозначается, то какую часть и куда мы будем поворачивать.


На изображениях не закрашенные гранями (квадратиками), являются те квадраты, фиксировать которые мы пока не собираемся.
Каждый из этапов сборке подробно изображён на картинках.
Прежде чем начинать крутить кубик по схемам, договоримся, что верхней у нас будет всегда часть с центральным синим квадратом. Квадратик же находящийся под эти синим квадратиком, с противоположной стороны, в разных версиях Кубика Рубика, бывает разного цвета. Предположим, что он зелёный. По ходу сборки верхняя часть куба, должна стать у нас синей, а нижняя зелёной. Передняя грань будет любая, из оставшихся четырёх боковых сторон.
Если вы хоть раз держали кубик в руках, то хотя бы слегка понимаете, как он работает, и понимаете, что от вас требуется, а это значит, что сборку нужно производить так что бы каждая грань кубика примыкала к центральному квадратику того же цвета.
Кубик мы соберём в несколько этапов. Первые два этапа – нижний слой. Третий этап - средняя часть куба. Последние четыре этапа – верхний слой.

Что ж, приступим! Первый Этап.
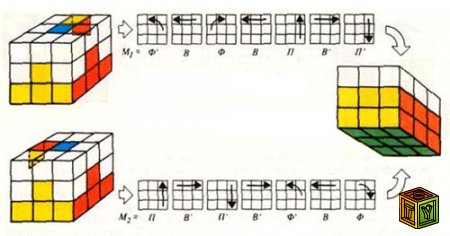
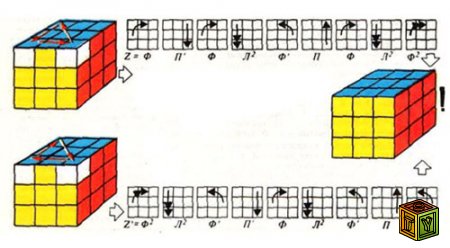
Крест снизу: Выбирите любой из зелёных квадратов, находящихся по краям кубика, который не находится в окончательном положении. Поворотом грани, в которой он находится, отправьте его в верхнею грань. Предположим, что вторая часть выбранного кубика – жёлтая. Разворотом куба, сделайте передней грань с желтым нейтральным квадратом. И поворачивая верхнюю грань, приведите кубик в какое-то из 2-х положений изображенных на рисунке. Далее действуйте по схеме, и нижний кубик окажется там, где нужно. Помните о том, что дальнейшие ваши действия не должны портить достигнутого результата. Поразмышляйте над тем, как это можно реализовать.

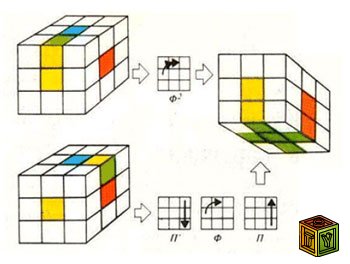
Рисунок 1
Далее на всех рисунках передняя часть куба будет изображаться жёлтым цветом. То есть с жёлтым центральным квадратом. Правую плоскость – красной. Следовательно, собирая кубик, вы должны сами принять для себя решение, какая грань будет передней.

Рисунок 2
Второй этап.
Четыре нижние грани: находим любой зелёный кубик в верхней боковой грани, находящийся в самом верху. Крутя верхнею грань, поверните его так, что бы он стал точно над своим местом снизу. При этом выбранный кубик займёт какое-то из положений, как на рисунке 2. Действуя по инструкции, куб окажется там, где нужно. Если же в верхнем слое больше нет кубов с зелёной гранью, но в нижнем слое кубик не стоит в окончательном положении, то нужно повернуть куб так чтобы он стал передним-правым-нижним. И далее проделать любую из операций на рисунке 2.

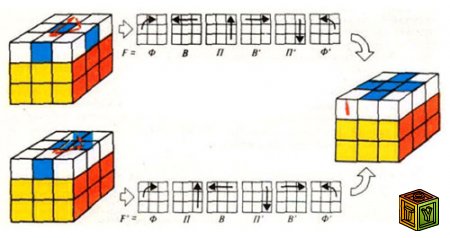
Рисунок 3
Средний слой: Выбирите любой из реберных граней без синих граней, расположенных в верхнем слое.
Вращая верхнюю грань, приведите кубик в положение, как и на рисунке 3. Действуйте по инструкции, и всё должно получиться.

Если же в верхнем слое больше нет реберных кубиков без синих граней, но есть кто-то из средних реберных кубиков не находится в окончательном положении, разверните куб так, чтобы он оказался “передним-правым”. И далее проделать любую из операций на рисунке 3.

Рисунок 4

Четвёртый этап.
Выставление верхних ребер кубика: ставим верхние боковые кубинки синими гранями вверх как на рисунке 4. Сделайте одно из 2-х действий на рисунке 4. Определённые кубики перевернутся, а так же они ещё и поменяются местами.

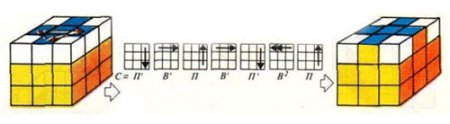
Рисунок 5

Пятый этап.
Меняем верхние реберные кубики: выставляем верхние реберные кубы на свои места, не переворачивая их как на рисунке 5. Если же какой-то из них уже расположен правильно, а три другие требуют перестановки по направлению часовой стрелки, как в случае А, выставьте куб в исходное положение, как на рисунке 5 и действуйте по схеме — кубы встанут на свои места. Второй вариант: прокрутите верхнюю грань таким образом, чтобы два ее реберных куба встали как нужно. Если же два других правильно не встанут, то дальше действуем по обстоятельствам, являются ли «правильные» кубики соседними (вариант Б или противоположными (вариант В). В вариант Б крутите верхнюю грань еще на 90° против часовой стрелки — должно получиться как вариант А. Если же выпал вариант В, делаем всё как на рисунке 5, передней будет любая боковая грань кубика; затем, повернув верхнюю грань на 90° в правильном направлении, опять придем к А.

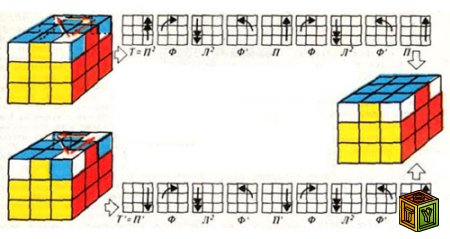
Рисунок 6
Шестой этап
Мы почти у цели. Поворачиваем верхние угловые кубики синими гранями вверх как на рисунке 6. Если три «неправильных» кубиков расположите кубик в одно из 2-х начальных положений рисунка 6 и далее действуем по инструкции — кубик развернётся.
В случае, когда нужно перевернуть 2 или 4 кубика, расположите так, чтобы левый верхний угол передней грани был синим и выполните действие “Т”.

Рисунок 7
Седьмой этап, заключающий.
Расставляем верхнею плоскость, не переворачивая их. А после шестого этапа может получиться несколько вариантов. Все кубы встали правильно, или же один из них встанет правильно, а ещё 3 нужно переставлять. Так же они все могут встать неправильно. Первый случай самый лучший, кубик Рубик собран правильно. Во втором варианте, смотря то, что нужно, нужно вращать кубы по часовой или же против часовой стрелке. Делаем один из 2-х шагов на рисунке 7. В случае три, проделываем любую операцию из рисунка 7 и получаем вариант 2.